Posting sebelumnya di SISTEM BINNER
Seperti pada bilangan desimal, dalam bilangan biner dapat dilakukan operasi aritmatika seperti penjumlahan, pengurangan, perkalian dan pembagian.
Penjumlahan Biner
Penjumlahan bilangan biner serupa dengan penjumlahan pada bilangan desimal. Dua bilangan yang akan dijumlahkan disusun secara vertikal dan digit-digit yang mempunyai signifikansi sama di tempatkan pada kolom yang sama. Digit-digit ini kemudian dijumlahkan dan jika jumlahnya lebih besar dari 1, maka ada bilangan yang disimpan, selanjutnya bilangan yang disimpan tersebut dijumlahkan dengan bilangan di sebelah kirinya.
Aturan dasar untuk penjumlahan pada bilangan biner adalah seperti berikut:
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 0, simpan 1
Sebagai contoh akan dijumlah dua bilangan biner 01012 + 00112 hasilnya 10002
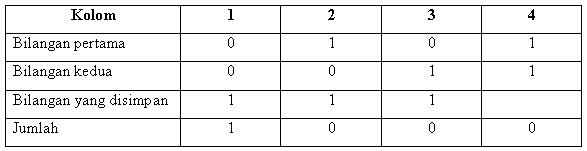Terkadang hasil penjumlahan bilangan lebih besar dari 2 jika hal
tersebut terjadi, maka bilangan dapat disimpan lebih dari satu tempat,
misalnya 1 + 1 + 1 +1 = 0 yang disimpan 10. Contoh soal 00012 + 00112 + 01012 + 01112 hasilnya 100002
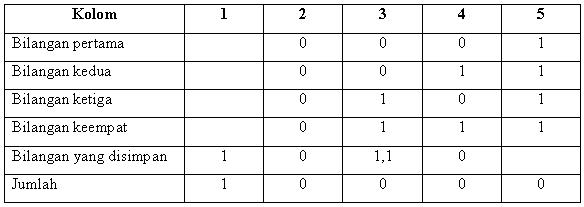Pada kolom ke 3, bilangan yang disimpan ada dua bilangan yang berasal
dari hasil penjumlahan pada kolom ke 5 yang nilai penjumlahannya adalah
(100) dan kolom ke 4 yang nilai penjumlahannya adalah (10). Sedangkan
bilangan yang disimpan pada kolom 1 dan 2 merupakan bilangan hasil dari
penjumlahan pada kolom 3 yang nilai penjumlahannya adalah (100).
Pengurangan Biner
Metode yang digunakan dalam pengurangan bilangan biner juga sama dengan metode yang digunakan untuk pengurangan pada bilangan desimal. Dalam metode ini, jika diperlukan sebuah angka diperbolehkan meminjam 1 dari kolom yang mempunyai derajat lebih tinggi atau yang biasanya berada di sebelah kiri.
Aturan dasar untuk pengurangan bilangan biner adalah sebagai berikut:
0 – 0 = 0
1 – 0 = 1
1 – 1 = 0
0 – 1 = 1, pinjam 1
Sebagai contoh terdapat dua bilangan biner x dan y bilangan x = 01012 , bilangan y = 00112. Jika dilakukan operasi pengurangan maka 01012 – 00112 hasilnya 00102, berikut penjelasannya:
- Pengurangan pada digit ke 4 dari x – y adalah 1 – 1 hasilnya 0.
- Pengurangan pada digit ke 3 dari x – y adalah 0 – 1 hasilnya 1, setelah angka 0 dari bilangan x meminjam angka 1 dari digit ke 2 dari bilangan x, sehingga digit ke 2 bilangan x berubah menjadi 0.
- Pengurangan pada digit ke 2 dari x – y adalah 0 – 0 hasilnya 0
- Pengurangan pada digit ke 1 dari x – y adalah 0 – 0 hasilnya 0
Perkalian Biner
Metode yang digunakan dalam perkalian biner juga pada dasarnya sama dengan perkalian desimal, akan terjadi pergeseran ke kanan setiap dikalikan 1 bit pengali. Setelah proses perkalian masing-masing bit pengali selesai, dilakukan penjumlahan masing-masing kolom bit hasil.
Contoh :
Pembagian Biner
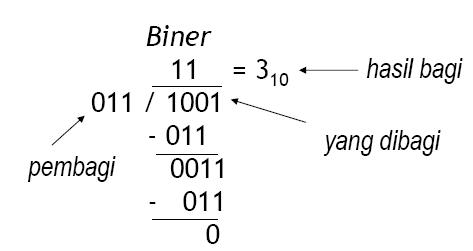
Serupa dengan perkalian, pembagian pada bilangan biner juga menggunakan metode yang sama dengan pembagian desimal. Bit-bit yang dibagi diambil bit per bit dari sebelah kiri. Apabila nilainya lebih dari bit pembagi, maka bagilah bit-bit tersebut, tetapi jika setelah bergeser 1 bit nilainya masih dibawah nilai pembagi maka hasilnya adalah 0.
Contoh :
Seperti pada bilangan desimal, dalam bilangan biner dapat dilakukan operasi aritmatika seperti penjumlahan, pengurangan, perkalian dan pembagian.
Penjumlahan Biner
Penjumlahan bilangan biner serupa dengan penjumlahan pada bilangan desimal. Dua bilangan yang akan dijumlahkan disusun secara vertikal dan digit-digit yang mempunyai signifikansi sama di tempatkan pada kolom yang sama. Digit-digit ini kemudian dijumlahkan dan jika jumlahnya lebih besar dari 1, maka ada bilangan yang disimpan, selanjutnya bilangan yang disimpan tersebut dijumlahkan dengan bilangan di sebelah kirinya.
Aturan dasar untuk penjumlahan pada bilangan biner adalah seperti berikut:
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 0, simpan 1
Sebagai contoh akan dijumlah dua bilangan biner 01012 + 00112 hasilnya 10002
Pengurangan Biner
Metode yang digunakan dalam pengurangan bilangan biner juga sama dengan metode yang digunakan untuk pengurangan pada bilangan desimal. Dalam metode ini, jika diperlukan sebuah angka diperbolehkan meminjam 1 dari kolom yang mempunyai derajat lebih tinggi atau yang biasanya berada di sebelah kiri.
Aturan dasar untuk pengurangan bilangan biner adalah sebagai berikut:
0 – 0 = 0
1 – 0 = 1
1 – 1 = 0
0 – 1 = 1, pinjam 1
Sebagai contoh terdapat dua bilangan biner x dan y bilangan x = 01012 , bilangan y = 00112. Jika dilakukan operasi pengurangan maka 01012 – 00112 hasilnya 00102, berikut penjelasannya:
- Pengurangan pada digit ke 4 dari x – y adalah 1 – 1 hasilnya 0.
- Pengurangan pada digit ke 3 dari x – y adalah 0 – 1 hasilnya 1, setelah angka 0 dari bilangan x meminjam angka 1 dari digit ke 2 dari bilangan x, sehingga digit ke 2 bilangan x berubah menjadi 0.
- Pengurangan pada digit ke 2 dari x – y adalah 0 – 0 hasilnya 0
- Pengurangan pada digit ke 1 dari x – y adalah 0 – 0 hasilnya 0
Perkalian Biner
Metode yang digunakan dalam perkalian biner juga pada dasarnya sama dengan perkalian desimal, akan terjadi pergeseran ke kanan setiap dikalikan 1 bit pengali. Setelah proses perkalian masing-masing bit pengali selesai, dilakukan penjumlahan masing-masing kolom bit hasil.
Contoh :
Pembagian Biner
Serupa dengan perkalian, pembagian pada bilangan biner juga menggunakan metode yang sama dengan pembagian desimal. Bit-bit yang dibagi diambil bit per bit dari sebelah kiri. Apabila nilainya lebih dari bit pembagi, maka bagilah bit-bit tersebut, tetapi jika setelah bergeser 1 bit nilainya masih dibawah nilai pembagi maka hasilnya adalah 0.
Contoh :
Print this page
